本文有关于各个激活函数局限性的描述.
本质上是提出了一个用于协同过滤的网络结构, 将MF的内积结构硬是变成了所谓的神经元结构(加权边 + 激活函数)
本文提出的MF(内积)导致的Limitation很有意思,如下图,文中提出的理由是latent vector 维度降低导致的, 所以适当提高其维度的可以解决,但可能造成另一个问题: 过拟合! 不过本文并不是采用提高维度的方法来解决的, 他是将内积形式变成了神经元结构, 这样就能解决MF(内积形式的)不足? 文中好像没有给出理由, 可能只是文章的噱头! (不过仔细想想, 文中模型中涉及 了核函数, 这个可能是提高latent vector维度的本质, 我不知道! 文中没有解释, 如果真是这样, MF也可以通过融入kernel的方法解决这个问题)
关于下图的解释, 见原文!
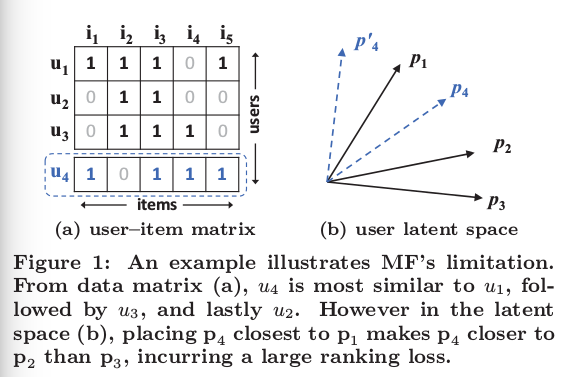
再来说说本文的model到底是怎样的, 如图
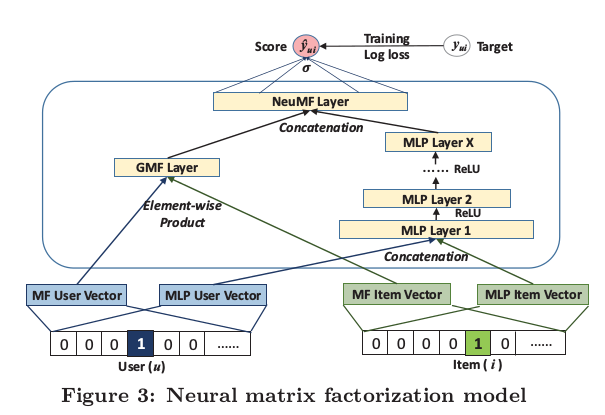
核心思想: 把原来的user和item的隐特征向量的每一维度都变成一个神经元. 再利用神经网络结构学习连接权和隐向量(奇怪的是,实际的输入也是不知道的,虽然作者偷换了概念,把输入定义成了one-hot 的向量), 不过反过来用MF学习参数的方法来理解本模型的话,也就觉得合理了, 因为输入都是两个隐向量,输出都是0或1. (这里正好指出,本文属于pointwise的方法,用了负样本采样)
细节部分: 上图模型分成两个部分: GMF和MLP (他们可以分别学出) , 值得注意的是:图中标出的 Element-wise product和Concatenation的区别; 后者有个神经元之间的交互,也就是作者说的, 融入了用户和item之间的交互信息.
实验部分: 待阅!
总结: 感觉本文没有什么实质的贡献, 除了耍了小聪明, 让模型看起来很复杂,很高级. 不过这也是DP文章通用的伎俩. 不过文中到底是怎么学习参数的,值得研究 (虽然作者没有具体指出)
| 文献题目 | 去谷歌学术搜索 | ||||||||||
| Neural Collaborative Filtering | |||||||||||
| 文献作者 | Xiangnan He; Hanwang Zhang | ||||||||||
| 文献发表年限 | 2017 | ||||||||||
| 文献关键字 | |||||||||||
| Collaborative Filtering, Neural Networks, Deep Learning, Matrix Factorization, Implicit Feedback; NeuMF | |||||||||||
| 摘要描述 | |||||||||||
| In recent years, deep neural networks have yielded immense success on speech recognition, computer vision and natural language processing. However, the exploration of deep neural networks on recommender systems has received relatively less scrutiny. In this work, we strive to develop techniques based on neural networks to tackle the key problem in recommendation — collaborative filtering — on the basis of implicit feedback. Although some recent work has employed deep learning for recommendation, they primarily used it to model auxiliary information, such as textual descriptions of items and acoustic features of musics. When it comes to model the key factor in collaborative filtering — the interaction between user and item features, they still resorted to matrix factorization and applied an inner product on the latent features of users and items. By replacing the inner product with a neural architecture that can learn an arbitrary function from data, we present a general framework named NCF, short for Neural network- based Collaborative Filtering. NCF is generic and can ex- press and generalize matrix factorization under its frame- work. To supercharge NCF modelling with non-linearities, we propose to leverage a multi-layer perceptron to learn the user–item interaction function. Extensive experiments on two real-world datasets show significant improvements of our proposed NCF framework over the state-of-the-art methods. Empirical evidence shows that using deeper layers of neural networks offers better recommendation performance. | |||||||||||