几个引导性问题
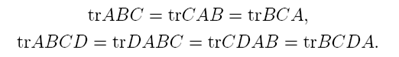
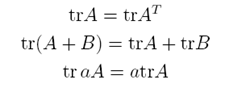
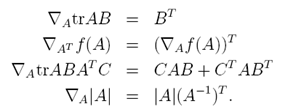
概念解释
An extreme case of K-fold cross-validation is where K=N, the number of observation in our dataset: each data observation is held out in turn and used to test a model trained on the other N-1 objects.
Fold1, Fold2, ... Fold k, 轮流对当做测试集, 若 |Fold i|=1则 为 LOOCV
LOOCV一般可以达到用大量测试据测试出的效果是一样的, 所以比较常用.
K-fold cross validation 主要是要给出一个公平的测试结果,从而比较不同model之间的好坏.
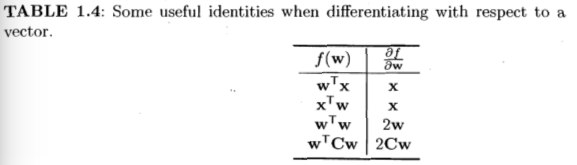
As we don't want our model to become too complex, it makes sense to try and keep sum of parameter squares low. So, rather than just minimising the average squared loss function, we could minimise a regularised loss function made by adding together our previous and a term penalising over-complexity.
If is too small, our function is likely to be too complex, Too large, and we will not capture any useful trends in the data.
| 文献题目 | 去谷歌学术搜索 | ||||||||||
| A First Course in Machine Learning - Linear Model: A Least Squares Approach | |||||||||||
| 文献作者 | Simon Rogers; Mark Girolami | ||||||||||
| 文献发表年限 | 2012 | ||||||||||
| 文献关键字 | |||||||||||
| Linear Model; least square; Leave one out cross validation | |||||||||||
| 摘要描述 | |||||||||||
| 机器学习入门书籍第一章,从最简单的线性模型讲起。 | |||||||||||