理解LDA: (核心:document-topic 概率矩阵, topic-word 概率矩阵, 采样生成document-topic概率分布向量的密度函数,采样生成topic-Word概率分布向量的密度函数)
(1) 所有文档的主题分布都服从同一个Dir(a)分布, 也就是把每个文档的主题分布当做一个具体的观测值, 那么它就是来自于Dir(a)的采样 (每一个维度代表一个主题在该文档中的概率)
(2) 一篇文档下的一个单词只会被分配给一个主题(即概率最大的那个主题); 但一个单词跟多个主题都有联系(学习的时候需要考虑)
(3) 在给单词分配主题时(即下面的第2步),理解上(拆分理解): 每次操作只会选取一个主题(即MultiNominal实验次数为1: one-hot向量; 这样就会趋向选择概率最大的主题),
(4) 将所有文档的所有单词形成一个vocabulary, 词语分布指的是vocabulary每个单词的概率(每个维度代表在该主题下,该单词的概率), 一个主题一个采样
(5) 同样,在以下第5步中,只做一次实验,形成一个one-hot的向量,one指向谁,就选择哪个单词(此时MultiNominal计算的值代表的是选择这个单词而不选择其他的单词的概率)
(6) 关于下面等式2-2靠近等号的第一个求积符号的疑惑,为什么是求积符号,而不是求和符号?原因: 根据K个主题和同一个分布,需要从分布中采样K次才能完成“主题-单词”概率分布矩阵。比(8)中展示的更详细
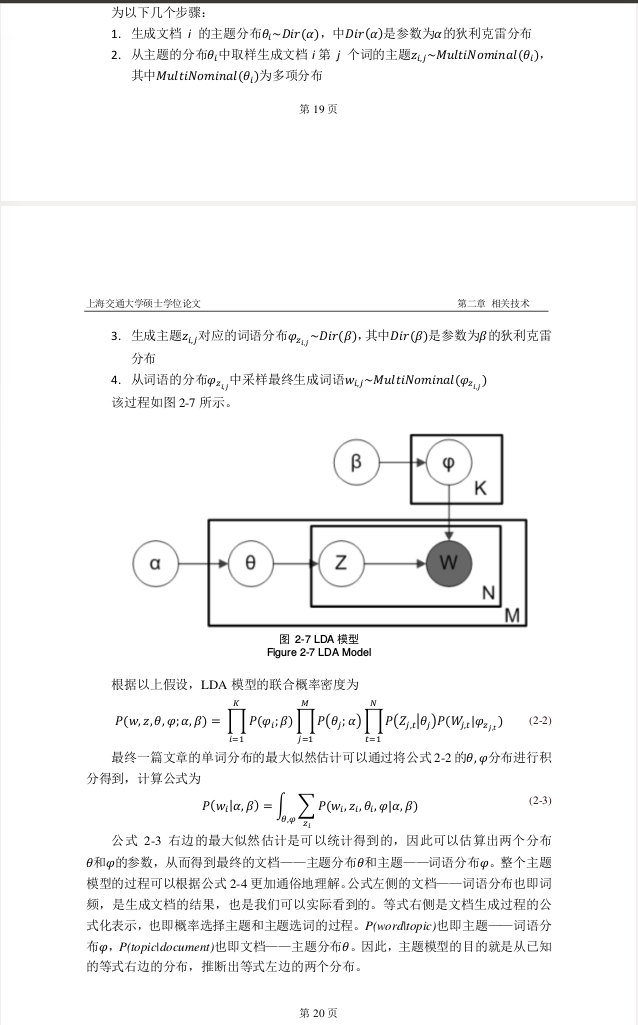
(7) 以下2-2公式中, K表示主题个数; M表示文档个数; N表示每个文档单词个数
(8) 强烈推荐ref: http://blog.csdn.net/huagong_adu/article/details/7937616 (尤其对帮助理解以上(6)问题很有用)
(9)公式2-2理解: 从左往右-> 根据 采样形成“主题-单词”概率分布矩阵事件的概率->对所有M个文档采样各自主题分布的概率-> 在确认了文档的主题分布之后,再确定单个单词的为某个主题的概率 x 该主题下该单词的概率; 最后以联合概率密度的形式把所有的事件同时发生的概率表达出来。
(10) 对4个概率生成步骤的理解:在每个步骤中的采样,我们都可以理解为所采样,都是使之概率最大的自变量,如1中采样使得最大;2中采样概率最大的主题;4中采样概率最大的单词;其中对于3的理解需要注意: 该步骤其实只进行了K次(主题个数,每个主题一次),而不是每个单词都重新计算,因为主题关于单词的分布是在整个语料库层面上的。

(1)如果我们已知每个文档里面每个词的主题,那么我就很容易通过极大似然的方法求得document-topic和topic-word两个关于概率的隐因子矩阵。(类似于矩阵分解,且可以直接推导出公式:
(2)问题是:我们不知道每个词的主题。所以我们基于已知概率分布(估计的),进行样本集的构造(抽样)
(3)ref: 为什么用吉布斯采样 :我们需要得到符合某种联合密度p(E,T,W)的样本集合,问题是我们不知道p(E,T,W)。当然,如果知道的话,就没有必要用gibbs sampling了。但是,我们知道三件事的conditional distribution。也就是说,p(E|T,W),p(T|E,W),p(W|E,T)。现在要做的就是通过这三个已知的条件分布,再用gibbs sampling的方法。在采样完成后,我们可以用这些样本来近似所有变量的联合分布。如果仅考虑其中部分变量,则可以得到这些变量的边缘分布。此外,我们还可以对所有样本求某一变量的平均值来估计该变量的期望。
(4)吉布斯采样的一般步骤: ref wiki-zh
(5)LDA中的吉布斯采样。由于在LDA中我们关注三个参数z,theta和phi。其中z是语料中每一个word对应的隐变量(主题),theta是语料中每一个文档的主题分布,phi是每一个主题的term分布。其实只要求得z,其他两个可以通过简单的似然估计得到。于是需要将LDA的概率公式P(w,z,theta,phi | alpha,beta)通过积分的方法把theta和phi积掉,剩下P(w,z | alpha,beta)。然后求解P(z|w,alpha,beta) = P(w,z | alpha,beta) / P(w | alpha,beta),由于分母要对K的n次方个项求和因此直接求不可行(其中K是主题数,n是词汇表的长度),即概率分布P(z|w,alpha,beta)的样本难以生成。Gibbs抽样就是要完成对P(z|w,alpha,beta)的抽样,利用抽样结果通过简单的似然估计求得theta和phi。 ref: http://www.cnblogs.com/maxiaoxin/p/3629327.html
(6)具体采样步骤:ref zn-wiki (wiki中的 -i 表示的是Word的补集,核心思想:给每个word分配topic,重新给每个Word分配topic,直到确定样本)
(7)给word分配主题,会引起(1)中两个变量的变化,在下一轮分配中,根据updated(1)中的两个变量,又反过来影响了word的主题分配。多次迭代后,可以求出(1)中的两个核心变量。以及利用统计的形式,可以确定topic-Word的统计矩阵。
(8)Word主题分配是如何影响(1)中的两个值的:ref 百度文库PDF(已经下载) 吉布斯采样概率转移公式推导(联合密度->条件概率密度)
(9)这种采用方式为什么能最优解化求解?(学习方向是正确的?): 每一次选择都是基于当前已知的边缘概率(假设为真实概率)做出的最优选择(边缘概率最大的topic选为为word的topic),不断迭代,就会越来越接近于真实概率,从而选出整体最优topic分配。
(10)利用生成过程得到的联合概率密度的作用: 通过积分的形式得到P(z,w)的联合密度函数,从而推导出吉布斯概率转移公式。 推荐 ref LDA数学八卦