正如本文题目所表示的那样, PMF实际上是MF的概率表达形式, 或者说在MF上加入了先验概率. 就像Least‐Mean‐Square (LMS) method 和 Probabilistic Interpretation of LMS 之间的关系.
Thus under independence assumption, LMS is equivalent to MLE of θ ! 所以, PMF和MF的本质是一样的,我想这一定也可以从librec实现PMF的代码中看出来.
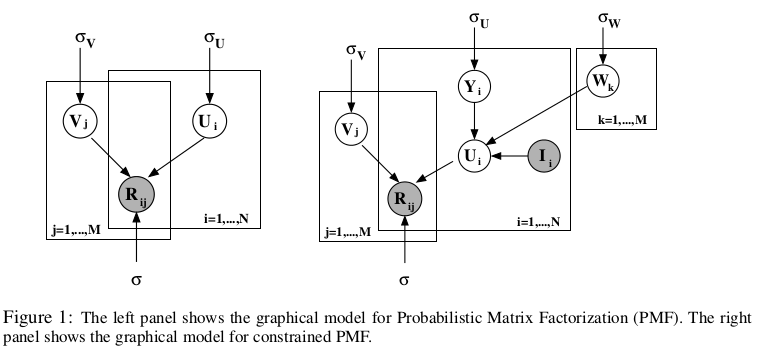
PMF和MF形式上的区别在于正则项. 但PMF的优势在于:引入了先验,相当于平滑了数据稀疏的问题,相当于在一定程度上解决了矩阵的稀疏问题; 另外概率图模型更利用文章的描述和model的表达,例如在变量U(user latent vector) 上加一层约束.(这也是刘师兄文章中的核心技巧,把利用label构建的相似关系约束进U和V,本质上,这种约束也可以通过MF加进去)
注意: 先验 p(U), 指示各个U的概率密度, 相当于从U的概率密度函数中抽取一个u. P(V) 亦然.
以下是PMF的核心公式和表达:
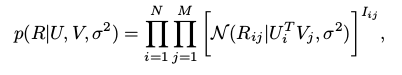
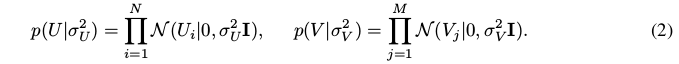
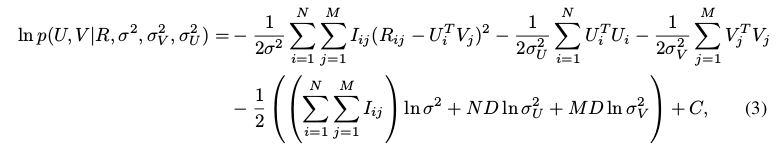
is equivalent to
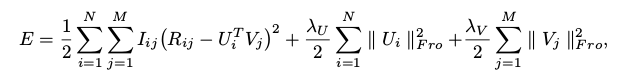
| 文献题目 | 去谷歌学术搜索 | ||||||||||
| Probabilistic Matrix Factorization | |||||||||||
| 文献作者 | Ruslan Salakhutdinov and Andriy Mnih | ||||||||||
| 文献发表年限 | 2008 | ||||||||||
| 文献关键字 | |||||||||||
| PMF; probabilisitc graphical model; 矩阵系数问题; sparse; sparsity; 1659 citation | |||||||||||
| 摘要描述 | |||||||||||
| Many existing approaches to collaborative filtering can neither handle very large datasets nor easily deal with users who have very few ratings. In this paper we present the Probabilistic Matrix Factorization (PMF) model which scales linearly with the number of observations and, more importantly, performs well on the large, sparse, and very imbalanced Netflix dataset. We further extend the PMF model to include an adaptive prior on the model parameters and show how the model capacity can be controlled automatically. Finally, we introduce a con- strained version of the PMF model that is based on the assumption that users who have rated similar sets of movies are likely to have similar preferences. The resulting model is able to generalize considerably better for users with very few ratings. When the predictions of multiple PMF models are linearly combined with the predictions of Restricted Boltzmann Machines models, we achieve an error rate of 0.8861, that is nearly 7% better than the score of Netflix’s own system. | |||||||||||